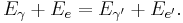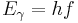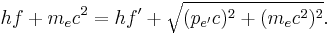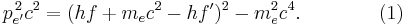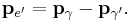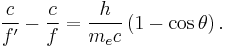Compton scattering

Compton scattering
Feynman diagrams
s-channel
u-channel
Light-matter interaction
Low energy phenomena	Photoelectric effect
Mid-energy phenomena	Compton scattering
High energy phenomena	Pair production

In physics, Compton scattering is a type of scattering that X-rays and gamma rays undergo in matter. The inelastic scattering of photons in matter results in a decrease in energy (increase in wavelength) of an X-ray or gamma ray photon, called the Compton effect. Part of the energy of the X/gamma ray is transferred to a scattering electron, which recoils and is ejected from its atom, and the rest of the energy is taken by the scattered, "degraded" photon.

Inverse Compton scattering also exists, where the photon gains energy (decreasing in wavelength) upon interaction with matter. Since the wavelength of the scattered light is different from the incident radiation, Compton scattering is an example of inelastic scattering, but the origin of the effect can be considered as an elastic collision between a photon and an electron. The amount the wavelength changes by is called the Compton shift. Although nuclear compton scattering exists^[1], Compton scattering usually refers to the interaction involving only the electrons of an atom. The Compton effect was observed by Arthur Holly Compton in 1923 at Washington University in St. Louis and further verified by his graduate student Y. H. Woo in the years following. Compton earned the 1927 Nobel Prize in Physics for the discovery.

The effect is important because it demonstrates that light cannot be explained purely as a wave phenomenon. Thomson scattering, the classical theory of an electromagnetic wave scattered by charged particles, cannot explain low intensity shifts in wavelength (Classically, light of sufficient intensity for the electric field to accelerate a charged particle to a relativistic speed will cause radiation-pressure recoil and an associated Doppler shift of the scattered light^[2], but the effect would become arbitrarily small at sufficiently low light intensities regardless of wavelength.) Light must behave as if it consists of particles in order to explain the low-intensity Compton scattering. Compton's experiment convinced physicists that light can behave as a stream of particle-like objects (quanta) whose energy is proportional to the frequency.

The interaction between electrons and high energy photons (comparable to the rest energy of the electron, 511 keV) results in the electron being given part of the energy (making it recoil), and a photon containing the remaining energy being emitted in a different direction from the original, so that the overall momentum of the system is conserved. If the photon still has enough energy left, the process may be repeated. In this scenario, the electron is treated as free or loosely bound. Experimental verification of momentum conservation in individual Compton scattering processes by Bothe and Geiger as well as by Compton and Simon has been important in disproving the BKS theory.

If the photon is of lower energy, but still has sufficient energy (in general a few eV to a few KeV, corresponding to visible light through soft X-rays), it can eject an electron from its host atom entirely (a process known as the photoelectric effect), instead of undergoing Compton scattering. Higher energy photons (1.022 MeV and above) may be able to bombard the nucleus and cause an electron and a positron to be formed, a process called pair production.

1 Description of the phenomenon
- 1.1 Derivation of the scattering formula
2 Applications
- 2.1 Compton scattering
- 2.2 Inverse Compton scattering
3 See also
4 Notes
5 Further reading
6 External links

Description of the phenomenon

A photon of wavelength λ comes in from the left, collides with a target at rest, and a new photon of wavelength λ′ emerges at an angle θ.

By the early 20th century, research into the interaction of X-rays with matter was well underway. It was known that when a beam of X-rays is directed at an atom, an electron is ejected and is scattered through an angle θ. Classical electromagnetism predicts that the wavelength of scattered rays should be equal to the initial wavelength;^[3] however, multiple experiments found that the wavelength of the scattered rays was greater than the initial wavelength.^[3]

In 1923, Compton published a paper in the Physical Review explaining the phenomenon. Using the notion of quantized radiation and the dynamics of special relativity, Compton derived the relationship between the shift in wavelength and the scattering angle:

$\lambda' - \lambda = \frac{h}{m_e c}(1-\cos{\theta}),$

where

λ is the initial wavelength,

λ′ is the wavelength after scattering,

h is the Planck constant,

m_e is the mass of the electron,

c is the speed of light, and

θ is the scattering angle.

The quantity ^h⁄_{m_ec} is known as the Compton wavelength of the electron; it is equal to 2.43×10⁻¹² m. The wavelength shift λ′ − λ is at least zero (for θ = 0°) and at most twice the Compton wavelength of the electron (for θ = 180°).

Compton found that some X-rays experienced no wavelength shift despite being scattered through large angles; in each of these cases the photon failed to eject an electron.^[3] Thus the magnitude of the shift is related not to the Compton wavelength of the electron, but to the Compton wavelength of the entire atom, which can be upwards of 10 000 times smaller.

Derivation of the scattering formula

A photon γ with wavelength λ is directed at an electron e in an atom, which is at rest. The collision causes the electron to recoil, and a new photon γ′ with wavelength λ′ emerges at angle θ. Let e′ denote the electron after the collision.

From the conservation of energy,

$E_\gamma + E_e = E_{\gamma'} + E_{e'}.\!$

Compton postulated that photons carry momentum;^[3] thus from the conservation of momentum, the momenta of the particles should be related by

$\mathbf{p}_\gamma = \mathbf{p}_{\gamma'} + \mathbf{p}_{e'},$

assuming the initial momentum of the electron is zero.

The photon energies are related to the frequencies by

$E_{\gamma} = hf\!$

$E_{\gamma'} = hf'\!$

where h is the Planck constant. From the relativistic energy-momentum relation, the electron energies are

$E_e = m_ec^2\!$

$E_{e'} = \sqrt{(p_{e'}c)^2 + (m_ec^2)^2}.$

Along with the conservation of energy, these relations imply that

$hf + m_e c^2 = hf' + \sqrt{(p_{e'}c)^2 + (m_e c^2)^2}.\,$

Then

$p_{e'}^{\, 2}c^2 = (hf + m_{e}c^2- hf')^2-m_{e}^2c^4. \qquad\qquad (1) \!$

Energies of a photon at 500 keV and an electron after Compton scattering.

From the conservation of momentum,

$\mathbf{p}_{e'} = \mathbf{p}_\gamma - \mathbf{p}_{\gamma'}.$

Then by making use of the scalar product,

$\begin{align} p_{e'}^{\, 2} &= \mathbf{p}_{e'}\cdot\mathbf{p}_{e'} = (\mathbf{p}_\gamma - \mathbf{p}_{\gamma'}) \cdot (\mathbf{p}_\gamma - \mathbf{p}_{\gamma'}) \\ &= p_{\gamma}^{\, 2} + p_{\gamma'}^{\, 2} - 2 p_{\gamma}\, p_{\gamma'} \cos\theta. \end{align}$

Thus

$p_{e'}^{\, 2}c^2 = p_{\gamma}^{\, 2}c^2 + p_{\gamma'}^{\, 2}c^2 - 2c^2 p_{\gamma}\, p_{\gamma'} \cos\theta.$

The relation between the frequency and the momentum of a photon is pc = hf, so

$p_{e'}^{\, 2}c^2 = (h f)^2 + (h f')^2 - 2(hf)(h f')\cos{\theta}. \qquad\qquad (2)$

Now equating 1 and 2,

$(hf + m_e c^2-hf')^2 -m_e^{\, 2}c^4 = \left(h f\right)^2 + \left(h f'\right)^2 - 2h^2 ff'\cos{\theta}. \,$

$2 h f m_e c^2 - 2 h f' m_e c^2 = 2 h^2 f f' \left( 1 - \cos \theta \right). \,$

Then dividing both sides by 2hff′m_ec,

$\frac{c}{f'} - \frac{c}{f} = \frac{h}{m_ec}\left(1-\cos \theta \right). \,$

Since fλ = f′λ′ = c,

$\lambda'-\lambda = \frac{h}{m_ec}(1-\cos{\theta}). \,$

Applications

Compton scattering

The "foggy, translucent" appearance of the exterior body parts in this PET scan image is caused by Compton scattering of the annihilation gamma rays in the body tissue. The ever-present phenomenon is one of the major challenges in radiographic nuclear medicine.

Compton scattering is of prime importance to radiobiology, as it happens to be the most probable interaction of gamma rays and high energy X rays with atoms in living beings and is applied in radiation therapy.^[4]

In material physics, Compton scattering can be used to probe the wave function of the electrons in matter in the momentum representation.

Compton scattering is an important effect in gamma spectroscopy which gives rise to the Compton edge, as it is possible for the gamma rays to scatter out of the detectors used. Compton suppression is used to detect stray scatter gamma rays to counteract this effect.

Inverse Compton scattering

Inverse Compton scattering is important in astrophysics. In X-ray astronomy, the accretion disk surrounding a black hole is believed to produce a thermal spectrum. The lower energy photons produced from this spectrum are scattered to higher energies by relativistic electrons in the surrounding corona. This is believed to cause the power law component in the X-ray spectra (0.2-10 keV) of accreting black holes.

The effect is also observed when photons from the cosmic microwave background move through the hot gas surrounding a galaxy cluster. The CMB photons are scattered to higher energies by the electrons in this gas, resulting in the Sunyaev-Zel'dovich effect. Observations of the Sunyaev-Zel'dovich effect provide a nearly redshift-independent means of detecting galaxy clusters.

Some synchrotron radiation facilities scatter laser light off the stored electron beam. This Compton backscattering produces high energy photons in the MeV to GeV range^[5] subsequently used for nuclear physics experiments.

Notes

↑ P Christillin (1986). "Nuclear Compton scattering". J. Phys. G: Nucl. Phys. 12: 837–851. doi:10.1088/0305-4616/12/9/008. http://www.iop.org/EJ/abstract/0305-4616/12/9/008.
↑ http://www.lle.rochester.edu/pub/PhD_theses/Moore.pdf
↑ ^3.0 ^3.1 ^3.2 ^3.3 Taylor, J.R.; Zafiratos, C.D.; Dubson, M.A. (2004). Modern Physics for Scientists and Engineers (2nd ed.). Prentice Hall. pp. 136–9. ISBN 013805715X.
↑ Camphausen KA, Lawrence RC. "Principles of Radiation Therapy" in Pazdur R, Wagman LD, Camphausen KA, Hoskins WJ (Eds) Cancer Management: A Multidisciplinary Approach. 11 ed. 2008.
↑ http://www.lnf.infn.it/~levisand/graal/graal.html

External links

BIGS animation compton effect
Compton Scattering - Georgia State University
Compton Scattering Data - Georgia State University

Compton scattering

Contents

Description of the phenomenon

Derivation of the scattering formula

Applications

Compton scattering

Inverse Compton scattering

See also

Notes

Further reading

External links